Question

A company sells widgets. The amount of profit y made by the company is related to the selling price of each widgets x by the given equation. Using this equation find out the maximum amount of profit the company can make to the nearest dollar. Y=-x^2+64x-292

Answer 1

732

Explanation:

Formula: -b/2a

-64/2(-1)

-64/-2= 32

Then you substitute x for your answer

-(32)^2+64(32)-292

-1024+2048-292= 732

You can also go on demos and type in the equation. The answer will be the Y value on the vertex (top of the parabola)

Answer 2

The maximum amount of profit is 32

Explanation:

Given

`y=-x^2+64x-292`

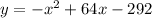
Required

Determine the maximum profit

This is calculated by calculating the maximum of the function.

A quadratic function is of the form

`y = ax^2 + bx + c`

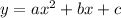
and its maximum is:

`Max = (-b)/(2a)`

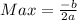
So:
`y=-x^2+64x-292`

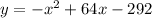
We have that

`a = -1`

`b = 64`

`c = -292`

`Max = (-b)/(2a)`

`Max = (-64)/(2 * -1)`

`Max = (-64)/(-2)`

`Max = 32`

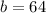
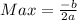
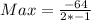
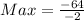
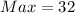
Hence, the maximum amount of profit is 32