Question

Given that f(x)= x^3/4 +6
a) Find f(4)
b) Find f^-1(x)
c) Find f^-1(8)

Answer 1

a)

`f(4)=(4^3)/(4)+6=4^2+6=16+6=22`

b)

`\begin{aligned}\\&y=(x^3)/(4)+6\\&4y=x^3+24\\&x^3=4y-24\\&x=\sqrt[3]{4y-24}\\&f^(-1)(x)=\sqrt[3]{4x-24}\end`

c)

`f^(-1)(8)=\sqrt[3]{4\cdot8-24}=\sqrt[3]{8}=2`

Answer 2

`\displaystyle \large{f(4)=22}\\\\\displaystyle \large{f^(-1)(x)=\sqrt[3]{4x-24}}\\\\\displaystyle \large{f^(-1)(8) = 2}`

Explanation:

In this problem, we are given the linear function:

`\displaystyle \large{f(x)=(x^3)/(4)+6}`

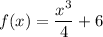
( a ) Find f(4)

Simply substitute x = 4 in the function f(x).

`\displaystyle \large{f(4)=(4^3)/(4)+6}\\\\\displaystyle \large{f(4)=4^2+6}\\\\\displaystyle \large{f(4)=16+6}\\\\\displaystyle \large{f(4)=22}`

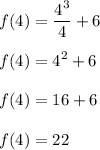
( b ) Find the inverse

To find
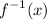`\displaystyle \large{f^(-1)(x)}`, solve for x-term then swap x-term and y-term.

`\displaystyle \large{4f(x)=x^3+24}\\\\\displaystyle \large{4f(x)-24=x^3}\\\\\displaystyle \large{\sqrt[3]{4f(x)-24}=\sqrt[3]{x^3}}\\\\\displaystyle \large{x=\sqrt[3]{4f(x)-24}}`

Swap f(x) and x.

`\displaystyle \large{f^(-1)(x)=\sqrt[3]{4x-24}}`

( c ) Find inverse f(8)

Substitute x = 8 in inverse function.

`\displaystyle \large{f^(-1)(8) = \sqrt[3]{4(8)-24}}\\\\\displaystyle \large{f^(-1)(8) = \sqrt[3]{32-24}}\\\\\displaystyle \large{f^(-1)(8) = \sqrt[3]{8}}\\\\\displaystyle \large{f^(-1)(8) = 2}`

Please let me know if you have any doubts!