What is the slope of a line perpendicular to the line whose equation is 6x+3y=-63

Question

asked May 2, 2021 178k views

2 Answers

Tasos Vogiatzoglou · Answer 1 · 2021-05-08T15:12:40+0000

Answer:

The slope of a line perpendicular to the line whose equation is 6x+3y=-63 will be: 1/2

Explanation:

We know that the slope intercept-form of the line equation is

y=mx+b

where m is the slope and b is the y-intercept

Given the equation

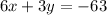
6x+3y=-63

simplifying the equation to write in the slope-intercept form

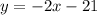
y=-2x-21

Thus, the slope = -2

As we know that the slope of the perpendicular line is basically the negative reciprocal of the slope of the line, so

The slope of the perpendicular line will be:

(-1)/(-2)=(1)/(2)

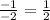
Therefore, the slope of a line perpendicular to the line whose equation is 6x+3y=-63 will be: 1/2