Question

Sum of infinite over E n=1 6(1/3)^n-1

Answer 1

`\displaystyle \large{\sum_(n=1)^\infty 6\left((1)/(3)\right)^(n-1) = (6)/(1-(1)/(3))}`

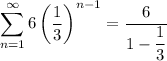
Explanation:

The given summation is infinite geometric series as it’s shown an exponent which geometric series/sequence has.

Let’s review partial geometric series formula:

`\displaystyle \large{S_n=(a_1(1-r^n))/(1-r)}`

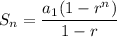
When we input the limit as n approaches infinity:

`\displaystyle \large{\lim_(n\to \infty) S_n = \lim_(n\to \infty) (a_1(1-r^n))/(1-r)}`

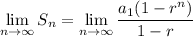
Consider each intervals.

( 1 ) When |r| > 1

Since |r| is greater than 1, it’s defined to approach infinity. Since it approaches infinity then we can say that the series diverges to infinity.

( 2 ) When r = 1

For r = 1, the equation for partial sum is S = na where a is first term and n is number of first term. For r = 1, the sum will continue to grow and will eventually approaches infinity. Henceforth, the series diverges.

( 3 ) When r ≤ -1

In this interval, the series oscillates which is defined to be divergent. Hence, the series diverges.

( 4 ) When |r| < 1

In this interval,
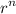`\displaystyle \large{r^n}` will approach 0 as accorded to exponential graph.

`\displaystyle \large{\lim_(n\to \infty) S_n = \lim_(n\to \infty) (a_1(1-0))/(1-r)}`

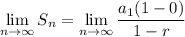
Hence, for |r| < 1, the geometric series will converge to:

`\displaystyle \large{\lim_(n\to \infty) S_n = (a_1)/(1-r)}`

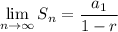
We can also write in summation notation form as:

`\displaystyle \large{\sum_(n=1)^\infty a_1r^(n-1) = (a_1)/(1-r)}`

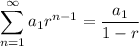
Therefore, from the given problem, it’s fortunately that the series is already in the same pattern as formula. Therefore, we simply apply the formula in.

`\displaystyle \large{\sum_(n=1)^\infty 6\left((1)/(3)\right)^(n-1) = (6)/(1-(1)/(3))}`

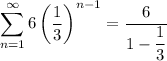
Therefore, the answer is third choice! Please let me know if you have any questions!