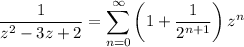Question

Find series expansion of 1/ z^2-3z+2 in region |z| <2

Answer 1

Expand the given expression into partial fractions.

`\frac1{z^2 - 3z + 2} = \frac1{(z-2)(z-1)} = \frac1{(2 - z) (1 - z)} = \frac1{1 - z} - \frac1{2 - z}`

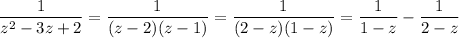
Recall the infinite geometric series,

`\displaystyle \sum_(n=0)^\infty z^n = \frac1{1-z}`

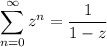
which converges in the unit disk |z| < 1.

The unit disk is a subset of the given region |z| < 2, so there are no issues with the convergence of series expansion of the first expression. For the second expression, we rearrange terms as

`\frac1{2 - z} = \frac12 * \frac1{1 - \frac z2}`

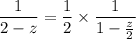
Then if |z/2| < 1, or equivalently |z| < 2, the series expansion for this term is

`\displaystyle \frac1{2-z} = \frac12 \sum_(n=0)^\infty \left(\frac z2\right)^n = \sum_(n=0)^\infty (z^n)/(2^(n+1))`

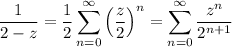
Putting everything together, the series expansion of the given expression over |z| < 2 is

`\displaystyle \frac1{z^2-3z+2} = \sum_(n=0)^\infty \left(1 + \frac1{2^(n+1)}\right) z^n`