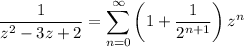Expand the given expression into partial fractions.
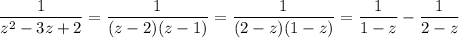
Recall the infinite geometric series,
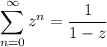
which converges in the unit disk |z| < 1.
The unit disk is a subset of the given region |z| < 2, so there are no issues with the convergence of series expansion of the first expression. For the second expression, we rearrange terms as
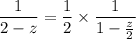
Then if |z/2| < 1, or equivalently |z| < 2, the series expansion for this term is
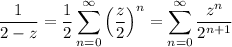
Putting everything together, the series expansion of the given expression over |z| < 2 is