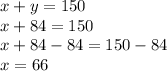Answer:
66 student tickets and 84 adult tickets
Explanation:
Write a system of equations. When writing the equation, group together amounts that have the same labels. You can only use the amounts in one equation and not both. I am going to use x to represent student tickets and y to represent adult tickets.
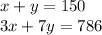
I am going to use elimination to solve. To do this, I am going to eliminate the x variable first. I am going to multiply the first equation by -3. I am doing this so the x's have the exact same number, but one of them is negative and one is positive, so when they are added they will equal zero.
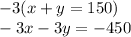
Your two new equations.
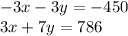
Now add and solve for y.
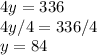
Now solve for x. I am going to use the first equation and substitute 84 for y.