Question

PLEASE PLEASE PLEASE HELP

Answer 1

a)

Growth rate 0.075

Growth factor 1.075

b) 59177 or approx 60000

Explanation:

I love these kind of question where we get to model equations :D So lets get started.

a)

The population of a city after t years after 2010 is given by

`P=20000(1.075)^t`

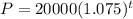
The original exponential growth formula is:

`y=a(1+r)^t`

so we can write our equation in this form as well:

`P=20000(1+0.075)^t`

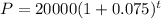
the growth factor is 1+r which is 1+0.075 which is 1.075

the growth rate is determined by the value of r which is 0.075

b)

Since our equation represents the population of a city after the year 2010 we can use it to further calculate the population in 2025 so

2025 - 2010 = 15

we set the value of t in our equation to 15 which is in years,

`P=20000(1.075)^(15)\\P=59177`

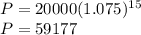
so we can say that our population in 2025 would be approximately 60,000