Answer:
a) y=5000e^{0.099t}
b) 11.097 hours
Explanation:
a
Many systems exhibit exponential growth. These systems follow a model of the form
 , where a represents the initial state of the system and k is a positive constant, called the growth constant.
, where a represents the initial state of the system and k is a positive constant, called the growth constant.
So we have our value of which represents the initial state of the system, which is 5000.
We need to calculate k.
Now,
It says he doubling time of a population of bacteria is 7 hours there are 5000 present initially, which means at 0 hours there were 5000 bacteria (initially means at t = 0, and then after 7 hours it doubled so it became 10,000 at 07:00 hours then at 14:00 it became 20,000 and then at 21:00 it became 40,000 this is the doubling time. So to calculate the value of k we can use this data, lets take 10,000 bacteria at 07:00 hours and put in our equation.
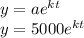
value of a is 5000 which was the initial value now we need the value of y which is the total amount of bacteria after t hours. So after 7 hours we have a total of 10,000 bacteria so our value of t becomes 7 and value of y becomes 10,000.

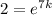
Apply natural logarithm on both sides
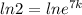
Ln e becomes 1 as we all know so we write 7k as it is.
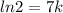
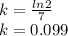
Now our equation is
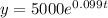
we can confirm this by inserting time t as 7 , 14 , 21 , 28 , 35 and we will get the exact bacteria we need which is y 10,000 , 20,000 , 40,000 , 80,000 , 160,000, respectively.
b)
It says how long will it take the population to triple which means the triple of 5000 is 15,000 and we set that to the value of y which is the amount of bacteria, and calculate t.
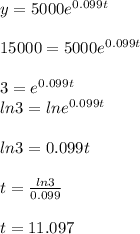
Which means it would take 11.097 hours for bacteria of 5000 to triple in size.