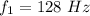Answer:
The fundamental frequency is
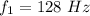
Step-by-step explanation:
From the question we are told that
The frequency of one harmonics is

The next higher harmonic is
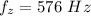
Generally the frequency of an air column open at both ends is mathematically represented as
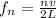
Here n is the order of the harmonics (frequency)
v is the velocity of the sound
L is the length of the column
So for one harmonics we have that
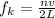
Then for the next higher harmonics
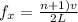
Generally the difference between these frequencies is mathematically represented as
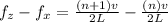
=>

=>
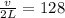
Generally for fundamental frequency n = 1
So

So
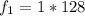
=>