Answer:
The average price of the stock over the first six years is 56.669 US dollars.
Explanation:
Since the price is a continuous and differentiable function, we can determine the average price by means of the following integral equation:
 (1)
(1)
Where:
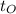 - Initial time, measured in years.
- Initial time, measured in years.
 - Final time, measured in years.
- Final time, measured in years.
If we know that
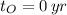 ,
,
 and
and
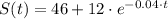 , then the average price of the stock over the first six years is:
, then the average price of the stock over the first six years is:
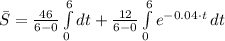
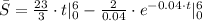 (2)
(2)
![\bar S = (23)/(3)\cdot (6-0)-(2)/(0.04)\cdot [e^(-0.04\cdot (6))-1]](https://img.qammunity.org/2021/formulas/mathematics/college/a7vfosanx8dkyyfmzhhgm7midrttppl8ur.png)
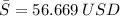
The average price of the stock over the first six years is 56.669 US dollars.