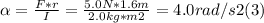Answer:
a) 4.0 rad/s2
Step-by-step explanation:
- For rigid bodies, Newton's 2nd law becomes :
τ = I * α (1)
where τ is the net external torque applied, I is the rotational inertia
of the body with respect to the axis of rotation, and α is the angular
acceleration caused by the torque.
- At the same time, we can apply the definition of torque to the left side of (1), as follows:
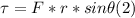
where τ = external net torque applied by Fnet, r is the distance
between the axis of rotation and the line of Fnet, and θ is the
angle between both vectors.
In this particular case, as Fnet is applied tangentially to the disk, Fnet
and r are perpendicular each other.
- Since left sides of (1) and (2) are equal each other, right sides are equal too, so we can solve for the angular acceleration as follows: