Answer:
1.736m/s²
Step-by-step explanation:
According to Newton's second law;
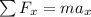
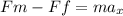 where;
where;
Fm is the moving force = 70.0N
Ff is the frictional force acting on the body
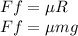
 is the coefficient of friction
is the coefficient of friction
m is the mass of the object
g is the acceleration due to gravity
a is the acceleration/deceleration
The equation becomes;
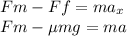
Substitute the given parameters
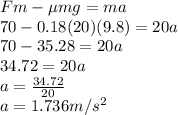
Hence the deceleration rate of the wagon as it is caught is 1.736m/s²