Answer:
![(-\infty, -4]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ru14lel5vc1lou8pzzrnomde2epfonuuh3.png)
Curved parenthesis at negative infinity
Square bracket at -4
====================================================
Work Shown:
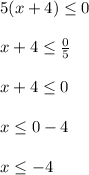
The last inequality shown above is the same as saying
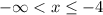
Converting this to interval notation leads to the final answer of
![(-\infty , -4]](https://img.qammunity.org/2021/formulas/mathematics/high-school/fn9ihda25pbn2225959r7y00wk76klp6s8.png)
Note the use of a square bracket at -4 to include this endpoint. We can never include either infinity, so we always use a parenthesis for either infinity.