Answer:
(a) Explained below.
(b) The 99% confidence interval for the difference between proportions is (-0.00094, 0.00494).
Explanation:
The information provided is:
n (Men who finished the marathon) = 25,221
n (Women who finished the marathon) = 12,883
Compute the proportion of men and women who finished the marathon as follows:
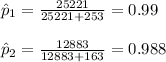
The combined proportion is:
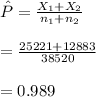
(a)
The hypothesis is:
H₀: The rate of those who finish the marathon is the same for men and women, i.e. p₁ - p₂ = 0.
Hₐ: The rate of those who finish the marathon is not same for men and women, i.e. p₁ - p₂ ≠ 0.
Compute the test statistic as follows:
![Z=\frac{\hat p_(1)-\hat p_(2)}{\sqrt{\hat P(1-\hat P)\cdot [(1)/(n_(1))+(1)/(n_(2))]}}](https://img.qammunity.org/2021/formulas/mathematics/high-school/hmj9k32076opql3f4hyr3oi1ke4j7t8t4r.png)
![=\frac{0.99-0.988}{\sqrt{0.989(1-0.989)*[(1)/(25474)+(1)/(13046)]}}\\\\=1.78](https://img.qammunity.org/2021/formulas/mathematics/high-school/scrxb702jgf5ojome3882kp0o1qkxuwoa1.png)
Compute the p-value as follows:
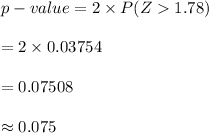
The p-value of the test is more than the significance level. The null hypothesis was failed to be rejected.
Thus, concluding that the rate of those who finish is the same for men and women.
(b)
Compute the 99% confidence interval for the difference between proportions as follows:
The critical value of z for 99% confidence level is 2.58.
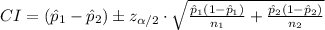
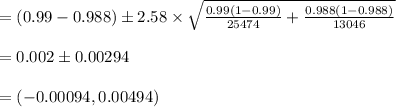
Thu, the 99% confidence interval for the difference between proportions is (-0.00094, 0.00494).