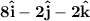Answer:
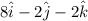
Step-by-step explanation:
Vectors in 3D
Given a vector
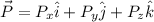
A vector
 parallel to
parallel to
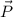 is:
is:
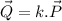
Where k is any constant different from zero.
We are given the vectors:
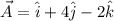
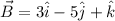
It's not specified what the 'resultant' is about, we'll assume it's the result of the sum of both vectors, thus:
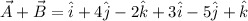
Adding each component separately:
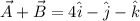
To find a vector parallel to the sum, we select k=2:
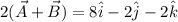
Thus one vector parallel to the resultant of both vectors is: