Explanation:
I'm going to explain this in standard slope intercept form (y=mx+b) because it is easiest for this situation. I will also include converting it to point slope form. I will also show how to do straight into point slope form if you find that more helpful.
First thing is to identify difference in x and y in both points. From point 1 to point to, the x changes -4 and the y changes +4. We can rapresent this in rise over run fraction
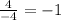
So the slope is -1 because the slope is the simplified rise over run fraction.
Our next step is to find the y-intercept. This is easy because the first point is the y-intercept, so -3 is our y-intercept.
Now we know the equation.
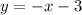
All we have to do now is convert it into point-slope form. So here is point slope form: y + y1 = m(x + x1). Y1 is the y-intercept and m is the slope.
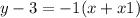
So x1 is the x intercept, so to find this you find the x value when y is 0. You can do this by using the standard form I've done because it is easiest.
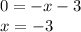
So when y is 0, then x is -3. Here is the complete point slope form of the line.
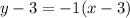
-----------------------------------------------------
To put the line directly into point slope for you need to find the slope, y-intercept, and x-intercept and place the values in accordingly. If you aren't given the y-intercept and x-intercept straight away it can be difficult for some putting it directly in point slope form. That is why I recommend putting it into standard form then point-slope form.