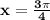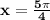Question

Solve cos x + √2 = -cos x for x over the interval [0, 2Π)

Answer 1

The correct answer is option C

Explanation:

Answer 2

`x=(3\pi)/(4)\\\\x=(5\pi)/(4)`

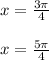
Explanation:

Trigonometric Equations

It's required to solve:

`\cos x+√(2)=-\cos x`

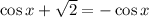
for
`x\in [0,2\pi)`

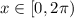
Adding cos x:

`2\cos x+√(2)=0`

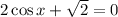
Subtracting
`√(2)`

`2\cos x=-√(2)`

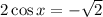
Dividing by 2:

`\displaystyle \cos x=-(√(2))/(2)`

Solving for x:

`\displaystyle x=\arccos\left(-(√(2))/(2)\right)`

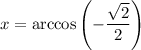
We need to find the angles whose cosine is
`-(√(2))/(2)` over the given interval.

These angles lie on the quadrants III and IV respectively and they are:

x=135°, x=225°

Converting to radians:

135 * π / 180 = 3π/4

225 * π / 180 = 5π/4

The two solutions are:

`\mathbf{x=(3\pi)/(4)}`

`\mathbf{x=(5\pi)/(4)}`