Question

Assume y≠60 which expression is equivalent to (7sqrtx2)/(5sqrty3)

Answer 1

The equivalent will be:

`\frac{\sqrt[7]{x^2}}{\sqrt[5]{y^3}}=\left(\:x^{(2)/(7)}\right)\left(y^{-(3)/(5)}\right)`

Therefore, option 'a' is true.

Explanation:

Given the expression

`\frac{\sqrt[7]{x^2}}{\sqrt[5]{y^3}}`

Let us solve the expression step by step to get the equivalent

`\frac{\sqrt[7]{x^2}}{\sqrt[5]{y^3}}`

as

`\sqrt[7]{x^2}=\left(x^2\right)^{(1)/(7)}` ∵
`\mathrm{Apply\:radical\:rule}:\quad \sqrt[n]{a}=a^{(1)/(n)}`

`\mathrm{Apply\:exponent\:rule:\:}\left(a^b\right)^c=a^(bc),\:\quad \mathrm{\:assuming\:}a\ge 0`

`=x^{2\cdot (1)/(7)}`

`=x^{(2)/(7)}`

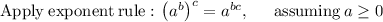
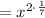
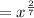
also

`\sqrt[5]{y^3}=\left(y^3\right)^{(1)/(5)}` ∵
`\mathrm{Apply\:radical\:rule}:\quad \sqrt[n]{a}=a^{(1)/(n)}`

`\mathrm{Apply\:exponent\:rule:\:}\left(a^b\right)^c=a^(bc),\:\quad \mathrm{\:assuming\:}a\ge 0`

`=y^{3\cdot (1)/(5)}`

`=y^{(3)/(5)}`

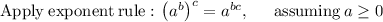
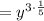
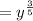
so the expression becomes

`\frac{x^{(2)/(7)}}{y^{(3)/(5)}}`

`\mathrm{Apply\:exponent\:rule}:\quad \:a^(-b)=(1)/(a^b)`

`=\left(\:x^{(2)/(7)}\right)\left(y^{-(3)/(5)}\right)` ∵
`\:\frac{1}{y^{(3)/(5)}}=y^{-(3)/(5)}`

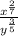
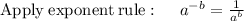
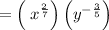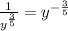
Thus, the equivalent will be:

`\frac{\sqrt[7]{x^2}}{\sqrt[5]{y^3}}=\left(\:x^{(2)/(7)}\right)\left(y^{-(3)/(5)}\right)`

Therefore, option 'a' is true.