Question

Find the slope of the line that passes through (4,2) and (9,1)?

Answer 1

Answer: m= -1/5

Explanation:

Find the Slope (4, 2) and (9, 1)

Slope is equal to the change in y over the change in x, or rise over run.

change in y

m = _________

change in x

The change in x is equal to the difference in x-coordinates (also called run), and the change in y is equal to the difference in y-coordinates (also called rise). y₂ − y₁

m = _____

x₂ − x₁

Substitute in the values of x and y into the equation to find the slope.

1 − (2)

m = _____

9 − (4)

Simplify the numerator.

−1

m = _____

9 − (4)

Simplify the denominator.

−1

m = _____

5

Move the negative in front of the fraction.

−1

m = _____

− 5

Answer 2

The slope of the line is
`\displaystyle -(1)/(5)`.

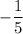Explanation:

We are given two coordinate points:

• 
  `(4, 2)`
• 
  `(9, 1)`

We are asked to find the slope of the line.

We can use the rise-over-run formula to solve for the slope of the line.

`\displaystyle \text{slope} = \frac{\text{rise}}{\text{run}}\\\\\text{slope} = (y_2-y_1)/(x_2-x_1)`

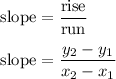
However, we firstly need to name our coordinate points.

In math, we can label our coordinates using the following label system:

`(x_1, y_1), (x_2, y_2)`

Therefore, we can also label our coordinates as such:

• 
  `x_1 = 4`
• 
  `y_1 = 2`
• 
  `x_2 = 9`
• 
  `y_2 = 1`

Now, we can supply these values into the formula and solve for our slope, or a better known variable, m.

`\displaystyle m = (1 - 2)/(9 - 4)\\\\m = (-1)/(5)\\\\m = -(1)/(5)`

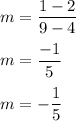
Therefore, our slope is
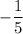`\displaystyle -(1)/(5)`.