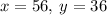Answer:
The numbers 'x' and 'y' are:
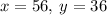
Explanation:
Let 'x' and 'y' be the two numbers
As the sum of the two numbers is 92.
so
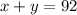
Given that One-eighth of the larger number plus one-third of the smaller number is 19.
so
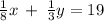
now solving both equations to determine the numbers 'x' and 'y'.
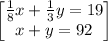
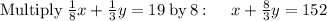
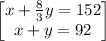
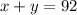

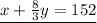
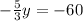
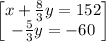
solve for y
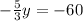
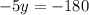
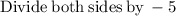
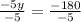
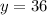
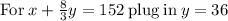
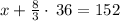
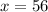
Thus, the numbers 'x' and 'y' are: