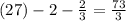Question

Evaluate (27)-2

-2/3
Express your answer as a fraction in simplest form.
The solution is

Answer 1

Note: The expression you have written sounds a little unclear, but I am assuming your expression is (27)-2-2/3.

So, I am solving the question based on assuming the expression as (27)-2-2/3, which would still clear your concept.

Answer:

The expression in the simplest form is:

`\left(27\right)-2-(2)/(3)=(73)/(3)`

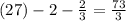
Explanation:

Given the expression

`\left(27\right)-2-(2)/(3)`

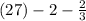
simplifying the expression in the simplest form

`\left(27\right)-2-(2)/(3)`

`=25-(2)/(3)`

`=(25\cdot \:3-2)/(3)`

`=(73)/(3)`

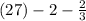
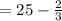
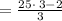
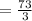
Thus, the expression in the simplest form is:

`\left(27\right)-2-(2)/(3)=(73)/(3)`