Answer:
The solution to the system of equations is
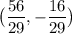 .
.
Explanation:
We are given a system of equations:
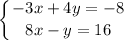
- We need to solve these by substitution, so we need to solve one equation for a variable and then substitute the value of that variable into the other equation.
- After doing this and solving for the opposite variable, we need to insert this into the original equation and solve for the initial variable.
- Therefore, to solve one of the equations, we will solve it to put it in slope-intercept form and solve for y. The easier equation to work with is equation two.
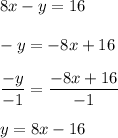
Now, we've solved for y. So, we can substitute this into either equation and solve for x.
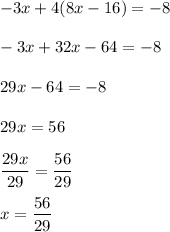
Now, we substitute our value for x into one of the original equations and solve for y.
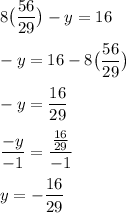
Therefore, the solution to our system of equations is: