Question

In ΔHIJ, h = 40 cm, ∠J=20° and ∠H=93°. Find the length of j, to the nearest centimeter.

Answer 1

Given:

In ΔHIJ, h = 40 cm, ∠J=20° and ∠H=93°.

To find:

The length of j, to the nearest centimeter.

Solution:

According to Law of sine,

`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

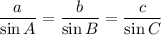
In ΔHIJ, using law of sine, we get

`(j)/(\sin J)=(h)/(\sin H)`

`(j)/(\sin (20^\circ))=(40)/(\sin (93^\circ))}`

`j=(40* \sin (20^\circ))/(\sin (93^\circ))}`

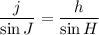
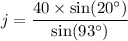
On further simplification, we get

`j=(40* 0.34202)/(0.99863)`

`j=(13.6808)/(0.99863)`

`j=13.69958`

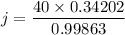
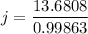
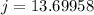
Approximate the value to the nearest centimeter.

`j\approx 14`

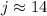
Therefore, the length of j is 14 cm.