Given:
In ΔHIJ, h = 40 cm, ∠J=20° and ∠H=93°.
To find:
The length of j, to the nearest centimeter.
Solution:
According to Law of sine,
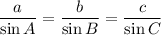
In ΔHIJ, using law of sine, we get
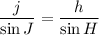
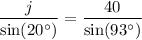
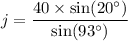
On further simplification, we get
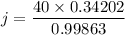
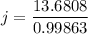
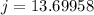
Approximate the value to the nearest centimeter.
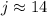
Therefore, the length of j is 14 cm.