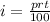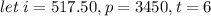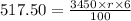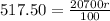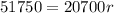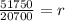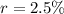Answer:
The answer is C.
Explanation:
First, you have to find the interest amount after 6 years. In order to do this, you have to subtract :
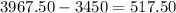
Next, you have to apply simple interest formula, I = (P×R×T)/100 where I repesents interest amount, P is priciple, R is interest rate and T is number of years :