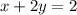Question

Line FG goes through the points (4,9) and (1,3). Which equation represents a line that is perpendicular to FG and passes through the point (2,0)?

-2x+ y=-4
-2x+y=2
X+2y=2
X+2y=4

Answer 1

X+2y=2

Explanation:

Answer 2

`x + 2y= 2`

Explanation:

Given

Points:

`F = (4,9)`

`G = (1,3)`

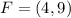
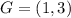
Required

Determine the equation of line that is perpendicular to the given points and that pass through
`(2,0)`

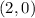
First, we need to determine the slope, m of FG

`m = (y_2 - y_1)/(x_2 - x_1)`

Where

`F = (4,9)` ---
`(x_1,y_1)`

`G = (1,3)` ---
`(x_2,y_2)`

`m = (3 - 9)/(1 - 4)`

`m = (- 6)/(- 3)`

`m =2`

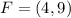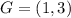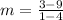
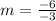
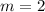
The question says the line is perpendicular to FG.

Next, we determine the slope (m2) of the perpendicular line using:

`m_2 = -(1)/(m)`

`m_2 = -(1)/(2)`

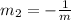
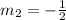
The equation of the line is then calculated as:

`y - y_1 = m_2(x - x_1)`

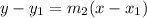
Where

`m_2 = -(1)/(2)`

`(x_1,y_1) = (2,0)`

`y - 0 = -(1)/(2)(x - 2)`

`y = -(1)/(2)(x - 2)`

`y = -(1)/(2)x + 1`

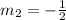
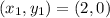
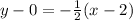
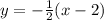
Multiply through by 2

`2y = -x + 2`

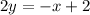
Add x to both sides

`x + 2y= -x +x+ 2`

`x + 2y= 2`

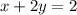
Hence, the line of the equation is
`x + 2y= 2`