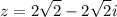Question

What complex number is represented by the polar coordinates (4, -pi/4)

Answer 1

`\displaystyle \large{z=2√(2) -2 √(2)i}`

Explanation:

A complex number is defined as z = a + bi. Since the complex number also represents right triangle whenever forms a vector at (a,b). Hence, a = rcosθ and b = rsinθ where r is radius (sometimes is written as |z|).

Substitute a = rcosθ and b = rsinθ in which the equation be z = rcosθ + irsinθ.

Factor r-term and we finally have z = r(cosθ + isinθ). How fortunately, the polar coordinate is defined as (r, θ) coordinate and therefore we can say that r = 4 and θ = -π/4. Substitute the values in the equation.

`\displaystyle \large{z=4[\cos (-(\pi)/(4)) + i\sin (-(\pi)/(4))]}`

Evaluate the values. Keep in mind that both cos(-π/4) is cos(-45°) which is √2/2 and sin(-π/4) is sin(-45°) which is -√2/2 as accorded to unit circle.

`\displaystyle \large{z=4\left((√(2))/(2) - (√(2))/(2)i \right)}\\\\\displaystyle \large{z=2√(2) -2 √(2)i}`

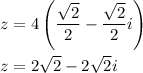
Hence, the complex number that has polar coordinate of (4,-45°) is
`\displaystyle \large{z=2√(2) -2 √(2)i}`