Question

What is the range of the function
f(x) = = 3x + 2 in the domain -2

Answer 1

The range is:

{-4, 1, 2, 5, 8}

Explanation:

Given the function

`f(x)=3x+2`

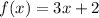
• We know that the domain of a function is the set of input or argument values for which the function is real and defined.

As the domain interval -2 ≤ x ≤ 2

i.e. the values in the domain = {-2, -1, 0, 1, 2}

• We also know that the range of a function is the set of values of the dependent variable for which a function is defined.

As the domain interval -2 ≤ x ≤ 2

Putting all the x-values in the domain interval in the function

so

putting x=-2 in the function

`f(x)=3x+2`

`f(-2)=3(-2)+2=-6+2=-4`

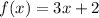
putting x=-1 in the function

`f(x)=3x+2`

`f(-1)=3(-1)+2=-3+2=1`

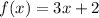
putting x=0 in the function

`f(x)=3x+2`

`f(0)=3(0)+2=0+2=2`

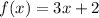
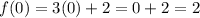
putting x=1 in the function

`f(x)=3x+2`

`f(1)=3(1)+2=3+2=5`

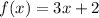
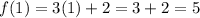
putting x=2 in the function

`f(x)=3x+2`

`f(2)=3(2)+2=6+2=8`

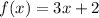
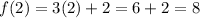
Thus, when we put the domain values, the corresponding range values are:

x y

-2 -4

-1 1

0 2

1 5

2 8

Therefore, the range is:

{-4, 1, 2, 5, 8}