Question

A simple off bacteria is debating according to the half life model. If the simple begins with 800 bacteria, and after 18 minutes there is 240 bacteria, after how many minutes will there be 40 remaining

Answer 1

After 43 minutes, the bacteria will be 40 remainings.

Explanation:

Given that:

Initial population of bacteria
`A_o` = 800

After time (t) = 18 mins

A = 240

Using the model:

`A = A_o e^(k*t)`

`240=800 e^(k*18)`

`(240)/(800)= e^(18k)`

`0.3= e^(18k)`

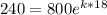
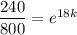
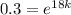
By applying natural log on both sides, we get:

In(0,3) = 18k (In e)

- 1.20397 = 18 k * (1)

18 k = -1.20397

k = -1.20397/ 18

k = - 0.06688

k ≅ -0.07

After time (t), the bacteria population (A) = 40

Now;

`40 = 800 e^(k*t)`

`(40 )/(800)= e^(-0.07*t)`

`0.05= e^(-0.07*t)`

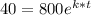
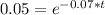
In (0.05) = -0.07t * In (e)

- 2.9957 = - 0.07t

t = - 2.9957/ -0.07

t = 42.795

t ≅ 43 minutes

Thus, after 43 minutes, the bacteria will be 40 remainings.