Answer:
After 43 minutes, the bacteria will be 40 remainings.
Explanation:
Given that:
Initial population of bacteria
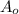 = 800
= 800
After time (t) = 18 mins
A = 240
Using the model:
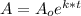
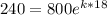
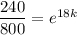
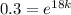
By applying natural log on both sides, we get:
In(0,3) = 18k (In e)
- 1.20397 = 18 k * (1)
18 k = -1.20397
k = -1.20397/ 18
k = - 0.06688
k ≅ -0.07
After time (t), the bacteria population (A) = 40
Now;
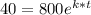
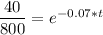
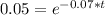
In (0.05) = -0.07t * In (e)
- 2.9957 = - 0.07t
t = - 2.9957/ -0.07
t = 42.795
t ≅ 43 minutes
Thus, after 43 minutes, the bacteria will be 40 remainings.