Question

In a production process, the probability of manufacturing a defective rear view mirror for a car is 0.075. Assume that the quality status of any rear view mirror produced in this process is independent of the status of any other rear view mirror. A quality control inspector is to examine rear view mirrors one at a time to obtain three defective mirrors. Determine the probability that the third defective mirror is the 10th mirror examined.

Answer 1

The probability that the 3rd defective mirror is the 10th mirror examined = 0.0088

Explanation:

Given that:

Probability of manufacturing a defective mirror = 0.075

To find the probability that the 3rd defective mirror is the 10th mirror examined:

Let X be the random variable that follows a negative Binomial expression.

Then;

`X \sim -ve \ Bin (k = 3 , p = 0.075)\\ \\ P(X=x)= \bigg (^(x-1)_(k-1)\bigg)* P^k* (1-P)^(x-k)`

`= \bigg (^(10-1)_(3-1)\bigg)* 0.075^3* (1-0.075)^(10-3)`

`= \bigg (^9_2\bigg)* 0.075^3* (1-0.075)^(7)`

`= (9!)/(2!(9-2)!)* 0.075^3* (0.925)^(7)`

`= (9*8*7!)/(2!(7)!)* 0.075^3* (0.925)^(7)`

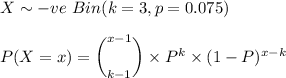
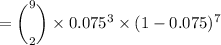
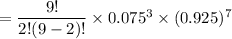
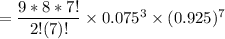
= 0.0087999

≅ 0.0088