Answer:
The probability of choosing a black counter is 0.25.
Also the picture is attached for the mark on scale.
Explanation:
Probability is the likeliness of occurrence of an event.
Given
There are three white and 1 black counter in the bag which means our sample space contains 3+1 = 4 elements
n(S) = 4
Let B be the event that the drawn out counter is black. As there is only one black counter
n(B) = 1
The probability of choosing a black counter is:
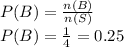
Hence,
The probability of choosing a black counter is 0.25.
Also the picture is attached for the mark on scale.