Question

3. Two cars are parked, 150m apart, and on opposite sides of a building. A camera on the top of the building rotates and can view both cars. One car can be viewed at an angle of depression of 370, and the other car can be viewed at an angle of depression of 420. How tall is the building?

Answer 1

The building is 61.5 m tall

Explanation:

The image below is a diagram where all the given distances and angles are shown. We have additionally added some variables:

h = height of the building

a, b = internal angles of each triangle

x = base of each triangle

The angles a and b can be easily found by subtracting the given angles from 90° since they are complementary angles, thus:

a = 90° - 37° = 53°

b = 90° - 42° = 48°

Now we apply the tangent ratio on both triangles separately:

`\displaystyle \tan a=\frac{\text{opposite leg}}{\text{adjacent leg}}`

`\displaystyle \tan 53^\circ=(150-x)/(h)`

`\displaystyle \tan 48^\circ=(x)/(h)`

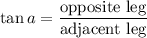
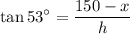
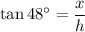
From the last equation:

`x=h.\tan 48^\circ`

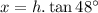
Substituting into the first equation:

`\displaystyle \tan 53^\circ=(150-h.\tan 48^\circ)/(h)`

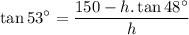
Operating on the right side:

`\displaystyle \tan 53^\circ=(150)/(h)-\tan 48^\circ`

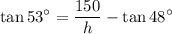
Rearranging:

`\displaystyle \tan 53^\circ+\tan 48^\circ=(150)/(h)`

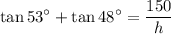
Solving for h:

`\displaystyle h=(150)/(\tan 53^\circ+\tan 48^\circ)`

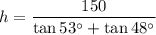
Calculating:

h = 61.5 m

The building is 61.5 m tall