Answer:
- The value of k is 12.57
- Radius of a seventeenth-century cannonball is 2.999 inches which can be rounded off to 3
Explanation:
Let s be the surface area and r be the radius
Then according to given statement
s∝r²
Removing the proportionality symbol introduces k, the constant of proportionality
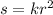
Now
A soap bubble with a 0.75 in. radius has a surface area of approximately 7.07 square inches.
Putting in the equation
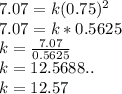
The euqation beomes
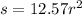
Putting s = 113.1 in the equation
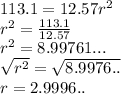
Hence,
- The value of k is 12.57
- Radius of a seventeenth-century cannonball is 2.999 inches which can be rounded off to 3