Question

What is the area of triangle ABC if a = 10 (degrees), B = 22 (degrees), and C = 70 (degrees) please help me.

A. 454.32 Sq Units
B. 103.37 Sq Units
C. 1.76 Sq Units
D. 17.61 Sq Units

Answer 1

D. 17.61 square units

Explanation:

To find the area of the ∆ABC, we can apply the formula below:

Area of ∆ABC = ½×a×c×sin(B)

a = 10

c = ??

B = 22°

Let's find c using Sine Rule:

Thus:

`(a)/(sin(A)) = (c)/(sin(C))`

Where,

a = 10

c = ??

A = 180 - (22 + 70) = 88°

C = 70°

Plug in the values

`(10)/(sin(88)) = (c)/(sin(70))`

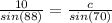
Multiply both sides by sin(70)

`(10)/(sin(88)) * sin(70) = (c)/(sin(70)) * sin(70)`

`(10 * sin(70))/(sin(88)) = c`

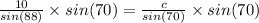
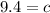`9.4 = c` (nearest tenth)

✔️Area of ∆ABC = ½×a×c×sin(B)

Plug in the values

Area of ∆ABC = ½ × 10 × 9.4 × sin(22)

Area = 17.61 square units (nearest tenth)