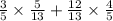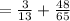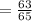If sinA 3/5 and cos B 5/13 , then find the value of sin (A+B)

Question

asked Dec 7, 2021 11.8k views

1 Answer

Laokoon · Answer 1 · 2021-12-12T05:01:12+0000

Answer:

(63)/(65)

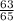
Explanation:

We have to find the value of sinB & cosA . So to find the value of sinB , let's use the identity

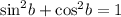
${ \sin }^(2) b + { \cos }^(2) b = 1$

By using the identity above gives

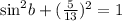
${ \sin}^(2) b + ( { (5 )/(13) })^(2) = 1$

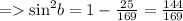
$= > { \sin}^(2) b = 1 - (25)/(169) = (144)/(169)$

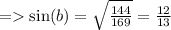
$= > \sin(b) = \sqrt{ (144)/(169) } = (12)/(13)$

Now to find the value of cosA , we'll use the same identity.

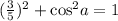
${( (3)/(5) })^(2) + { \cos}^(2) a = 1$

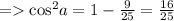
$= > { \cos }^(2) a = 1 - (9)/(25) = (16)/(25)$

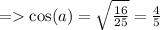
$= > \cos(a) = \sqrt{ (16)/(25) } = (4)/(5)$

Now we know that

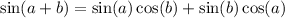
$\sin(a + b)=\sin(a)\cos(b)+\sin(b) \cos(a)$

So value of sin(a+b) =

(3)/(5) * (5)/(13) + (12)/(13) * (4)/(5)

= (3)/(13) + (48)/(65)

= (63)/(65)