Answer:
The linear speed of the car is approximately 27.30 m/s
Step-by-step explanation:
The question parameters are;
The mass of the person on the rollercoaster, m = 57.0 kg
The radius of the rollercoaster track, r = 42.7 m
The normal force felt by the person, F = 995 N
The centripetal force acting on the person keep the circular motion is given by the following equation;
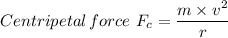
Where;
v = The linear velocity of motion = The linear speed of the car
The centrifugal force, F, is the force normal force felt by the person and is equal to the centripetal force, therefore, we have;

From which we have;
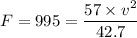
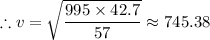
The linear speed of the car = v ≈ 27.30 m/s
The angular speed of the car, ω = v/r ≈ 27.30/42.7 ≈ 0.639 rad/s