Question

I needs help with it ​

Answer 1

a) initial height = 0 m

b) 8 s

c) vertex = (4, 32)

maximum height = 32 m

Explanation:

Given equation:

`h=-2t^2+16t`

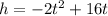
where:

• h is the height of the arrow about the ground (in metres)
• t is the time (in seconds)

Part (a)

The initial height of the arrow will be at the beginning of its journey, so when t = 0

Substitute t = 0 into the equation and solve for h:

`\implies h=-2(0)^2+16(0)`

`\implies h=0`

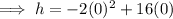
Therefore, the initial height of the arrow is 0 m.

Part (b)

The arrow will hit the ground when the height is 0 m.

Substitute h = 0 into the given equation:

`\implies -2t^2+16t=0`

Factor out -2t:

`\implies -2t(t-8)=0`

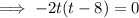
Therefore:

`\implies -2t=0 \implies t=0`

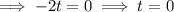
And:

`\implies t-8=0 \implies t=8`

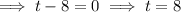
Therefore, the arrow will hit the ground at 8 seconds.

Part (c)

The vertex is the turning point of a parabola - it's minimum or maximum point.

As the leading coefficient for the given equation is negative, the parabola opens downwards and so its vertex is its maximum point.

There are different ways to find the vertex of a parabola. The easiest way to find the x-coordinate is by calculating the midpoint of the x-intercepts.

We have determined that the arrow has a height of 0 m at 0 seconds and 8 seconds. Therefore, t = 0 and t = 8 are the x-intercepts. The midpoint is halfway between zero and 8, so the midpoint is t = 4

To find the y-coordinate, substitute t = 4 into the equation and solve for h:

`\implies h=-2(4)^2+16(4)`

`\implies h=-32+64`

`\implies h=32`

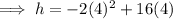
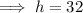
Therefore, the coordinates of the vertex are (4, 32)

The maximum height is the y-coordinate of the vertex.

Therefore, the maximum height is 32 m