Answer:
a.)
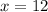
b.)
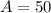
Explanation:
a.) Remember: the sum of all angles in a triangle will always be 180°.
Make an equation in which all given angles add up to 180:
∠1+∠2+∠3=180
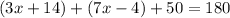
Solve the equation for the value of x. Remove the parentheses:
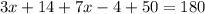
Combine like terms:
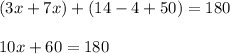
Subtract 60 from both sides:
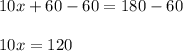
Divide both sides by 10:
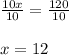
The value of x is 12.
b.) Insert the value of x into the given value of ∠A:
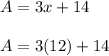
Simplify multiplication:
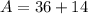
Add:
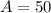
∠A is 50°.
:Done
Check Your Work:
To make sure the given values are true, solve for ∠B:
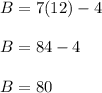
Now add all angle values to determine if they add up to 180°:
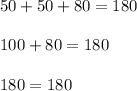
Since 180 is equal to 180, the values are true.