♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
_________________________________
Hint :
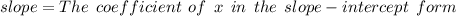
_________________________________
Thus we need to find the slope-intercept form of the line which must be like this :
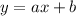
Let's do it...
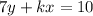
Subtract sides kx
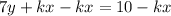
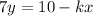
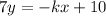
Divide sides by 7
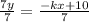
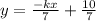
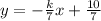
This is the slope-intercept form .

The slope is 3 ,
Thus :
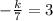
Multiply sides by 7
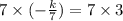
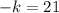
Multiply sides by - 1
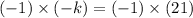
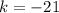
And we're done....
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️