Answer:
Equation of line b in standard form is:

Option A is correct.
Explanation:
We need to find equation of line b that passes through the point ( (6,4) and has a slope of -2.
First we need to find y-intercept of line using formula:
 where m is slope and b is y-intercept.
where m is slope and b is y-intercept.
Using m=-2 , x=6 and y=4 the y-intercept will be:
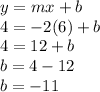
Now finding the equation of line having slope m=-2 and y-intercept b=-11
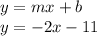
Writing the equation in standard form
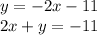
So, equation of line b in standard form is:

Option A is correct.