Question

Line b passes through the point ( (6,4) and has a slope of -2. What is the equation of Line b in standard form?

2x + y = -11
x + 2y = -14
x + 2y = -16
2x + y = 16

Answer 1

Equation of line b in standard form is:
`\mathbf{2x+y=-11}`

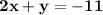
Option A is correct.

Explanation:

We need to find equation of line b that passes through the point ( (6,4) and has a slope of -2.

First we need to find y-intercept of line using formula:
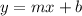`y=mx+b` where m is slope and b is y-intercept.

Using m=-2 , x=6 and y=4 the y-intercept will be:

`y=mx+b\\4=-2(6)+b\\4=12+b\\b=4-12\\b=-11`

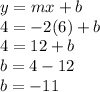
Now finding the equation of line having slope m=-2 and y-intercept b=-11

`y=mx+b\\y=-2x-11`

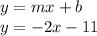
Writing the equation in standard form

`y=-2x-11\\2x+y=-11`

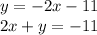
So, equation of line b in standard form is:
`\mathbf{2x+y=-11}`

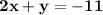
Option A is correct.