Question

A particle is projected in a straight line from a point O with a speed of
`6ms^-^1`. At time t sec later its acceleration is
`(1+2t)ms^-^2` . For the time when t =4 , calculate for the particle :

1. its velocity
2. its distance from O

P.S : This question should be solved using integration.

Answer 1

1. 26 m/s
2. 53 1/3 m

Explanation:

The speed will be the initial speed plus the integral of acceleration:

`\displaystyle v(t) = 6+\int_0^t{(1+2t)}\,dt=6+t+t^2\\\\v(t)=(t+1)t+6`

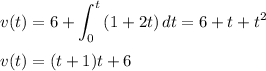
The position will be the integral of speed:

`\displaystyle p(t)=\int_0^t{v(t)}\,dt=6t+(1)/(2)t^2+(1)/(3)t^3\\\\p(t)=(((2t+3)t+36)t)/(6)`

__

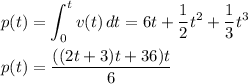
1. The velocity at t=4 is v(4) = (4+1)4 +6 = 26 m/s

2. The position at t=4 = ((2·4 +3)4 +36)4/6 = (44 +36)(2/3) = 160/3 = 53 1/3 m

At t=4, the particle will be 53 1/3 m from O and will be moving at a speed of 26 m/s.