Question

Calculus Application

2. A ladder 20 feet long leans a vertical building. If the bottom of the ladder slides away from the building
horizontally at a rate of 2 ft/sec, how fast is the ladder sliding down the building when the top of the
ladder is 12 feet above the ground?

Answer 1

-8/3 ft/s

Explanation:

We are given:

distance of the top of the ladder from the ground (h) = 12 ft

height of the ladder = 20 ft

rate of change of the distance of the base of ladder from the wall (dx/dt):

2 ft/s

Finding the distance of the base of the ladder from the wall:

From the Pythagoras's Theorem, we know that:

hypotenuse² = height² + base²

replacing the given values

20² = 12² + x²

400 = 144 + x²

x² = 256 [subtracting 144 from both sides]

x = 16 ft [taking the square root of both sides]

The rate of change of the height of the Ladder from the ground:

We know that:

h = 12 ft

(
`(dh)/(dt)`) = ?

x = 16 ft

(
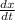`(dx)/(dt)`) = 2 ft/s

According to the Pythagoras's Theorem:

20² = x² + h²

differentiating both sides with respect to time

`(d(400))/(dt) = (d(x^(2) + h^(2)))/(dt)`

`0 = (d(x^(2)))/(dt) + (d(h^(2)))/(dt)`

`0 = (d(x^(2)))/(dx)((dx)/(dt)) + (d(h^(2)))/(dh)((dh)/(dt))`

`0 = 2x((dx)/(dt)) + 2h((dh)/(dt))`

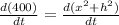
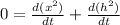
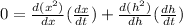
replacing the variables

`0 = 2(16)(2) + 2(12)((dh)/(dt))`

`0 = 64 + 32((dh)/(dt))`

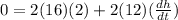
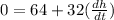
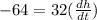`-64 =32((dh)/(dt))` [subtracting 64 from both sides]

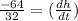`(-64)/(32) =((dh)/(dt))` [dividing both sides by 32]

`(dh)/(dt) = (-8)/(3) ft/s`

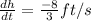
Hence, the ladder will slide down at a speed of 8/3 feet per second