Question

- a) The volume of a rectangular tank is (2a³ + a² - 2a - 1) cu. ft. where a>4 ft., the length is longer than its breadth and the breadth is longer than its height. (i) Find its length, breadth and height. (ii) Find the area of the its floor. ​

Answer 1

i) length > 9 ft

breadth > 5 ft

height > 3 ft

ii) Area of floor > 45 ft²

Explanation:

Volume of a rectangular prism

`\textsf{V}=lbh`

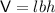
where:

• l is the length
• b is the breadth
• h is the height

Given:

• 
  `\sf V=(2a^3+a^2-2a-1)\:\:ft^3, \quad where\:a > 4\:ft`

Part (i)

To find expressions for the 3 dimensions of the tank, factor the expression for Volume.

Using the Factor Theorem, if V(x) = 0 then (a - p) is a factor:

`\implies \sf V(1)=2(1)^3+(1)^2-2(1)-1=0`

`\implies \sf V(-1)=2(-1)^3+(-1)^2-2(-1)-1=0`

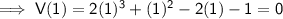
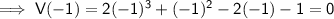
Therefore (a - 1) and (a + 1) are factors:

`\implies \sf 2a^3+a^2-2a-1=(a-1)(a+1)(2a+p)`

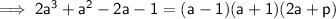
(where p is a constant to be found)

To find the value of p, expand:

`\implies \sf 2a^3+a^2-2a-1=2a^3+pa^2-2a-1`

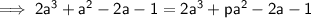
and compare coefficients:

`\implies \sf a^2=pa^2 \implies p=1`

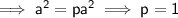
Therefore:

`\implies \sf 2a^3+a^2-2a-1=(a-1)(a+1)(2a+1)`

If l > b and b > h then:

• length (l) = (2a + 1)
• breadth (b) = (a + 1)
• height (h) = (a - 1)

If a > 4 ft then:

• length > 9 ft
• breadth > 5 ft
• height > 3 ft

Part (ii)

The area of the floor can be found by multiplying the found expressions for breadth and length:

`\begin{aligned}\implies \sf Area\:of\:floor & =(a+1)(2a+1)\\& = 2a^2+3a+1\end{aligned}`

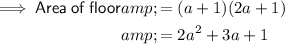
If a > 4 ft then Area of floor > 45 ft²

Answer 2

Given

The rectangle with:

• The volume of (2a³ + a² - 2a - 1) ft³, a > 4 ft
• The length > breadth > height

To find

• (i) the dimensions
• (ii) the area of the floor

Solution

(i)

Factorize the volume expression

• 2a³ + a² - 2a - 1 =
• 2a³ - 2a + a² - 1 =
• 2a(a² - 1) + (a² - 1) =
• (2a + 1)(a² - 1) =
• (a - 1)(a + 1)(2a + 1)

If a > 4, then:

• a - 1 > 4 - 1 ⇒ a - 1 > 3
• a + 1 > 4 + 1 ⇒ a + 1 > 5
• 2a + 1 > 2*4 + 1 ⇒ 2a + 1 > 9

Since the longest dimension is the length, it is

• 2a + 1

The breadth is the middle dimension, it is

• a + 1

The height is the smallest dimension, it is

• a - 1

(ii)

The area of the floor is:

• Area = length * breadth
• Area = (2a + 1)(a + 1) = 2a² + 3a + 1