Answer:
i) length > 9 ft
breadth > 5 ft
height > 3 ft
ii) Area of floor > 45 ft²
Explanation:
Volume of a rectangular prism
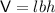
where:
- l is the length
- b is the breadth
- h is the height
Given:
Part (i)
To find expressions for the 3 dimensions of the tank, factor the expression for Volume.
Using the Factor Theorem, if V(x) = 0 then (a - p) is a factor:
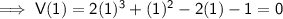
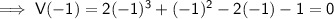
Therefore (a - 1) and (a + 1) are factors:
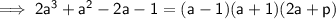
(where p is a constant to be found)
To find the value of p, expand:
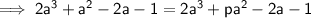
and compare coefficients:
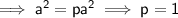
Therefore:
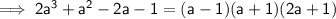
If l > b and b > h then:
- length (l) = (2a + 1)
- breadth (b) = (a + 1)
- height (h) = (a - 1)
If a > 4 ft then:
- length > 9 ft
- breadth > 5 ft
- height > 3 ft
Part (ii)
The area of the floor can be found by multiplying the found expressions for breadth and length:
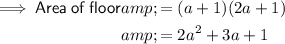
If a > 4 ft then Area of floor > 45 ft²