Answer:
The original length of each side of the equilateral triangle = x =15 inches
Explanation:
Let Original length of side of equilateral triangle = x
If it is increased by 5 inches, the length will become = x+5
Since in equilateral triangle all the ides have same length so,
New Length of side 1 = x+5
New of side 2 = x+5
New Length of side 3 = x+5
Perimeter of triangle = 60 inches
We need to find the value of x
The formula used is:
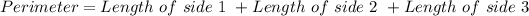
Putting values in formula and finding x
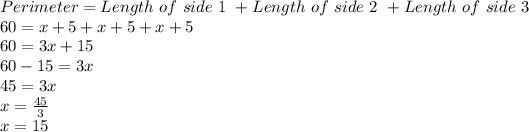
So, the original length of each side of the equilateral triangle = x =15 inches