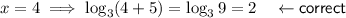Which equation is equivalent to log3(x+5) = 2

Question

asked Feb 13, 2023 32.7k views

2 Answers

Evren Kuzucuoglu · Answer 1 · 2023-02-19T08:08:44+0000

Answer:

3^2=x+5

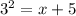
Explanation:

Given equation:

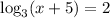
$\log_3(x+5)=2$

Method 1

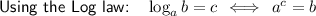
$\textsf{Using the Log law:} \quad \log_ab=c \:\: \Longleftrightarrow \:\: a^c=b$

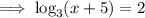
$\implies \log_3(x+5)=2$

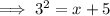
$\implies 3^2=x+5$

Method 2

Make both sides of the equation the index to base 3:

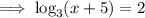
$\implies \log_3(x+5)=2$

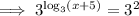
$\implies 3^(\log_3(x+5))=3^2$

Apply the log law
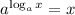$a^(\log_ax)=x$ :

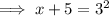
$\implies x+5=3^2$

Swap sides:

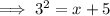
$\implies 3^2=x+5$

Solve for x

Although the question hasn't asked to solve for x, here is the solution:

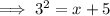
$\implies 3^2=x+5$

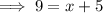
$\implies 9=x+5$

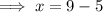
$\implies x=9-5$

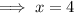
$\implies x=4$

Check

Substitute the found value of x into the original equation:

$x=4 \implies \log_3(4+5)=\log_39=2 \quad \leftarrow\textsf{correct}$