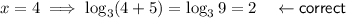Question

Which equation is equivalent to log3(x+5) = 2

Answer 1

`\\ \rm\Rrightarrow log_3(x+5)=2`

• log_a^b=c then b=a^c

`\\ \rm\Rrightarrow x+5=3^2`

`\\ \rm\Rrightarrow x+5=9`

`\\ \rm\Rrightarrow x=9-5`

`\\ \rm\Rrightarrow x=4`

Answer 2

`3^2=x+5`

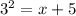
Explanation:

Given equation:

`\log_3(x+5)=2`

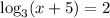
Method 1

`\textsf{Using the Log law:} \quad \log_ab=c \:\: \Longleftrightarrow \:\: a^c=b`

`\implies \log_3(x+5)=2`

`\implies 3^2=x+5`

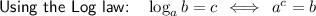
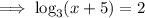
Method 2

Make both sides of the equation the index to base 3:

`\implies \log_3(x+5)=2`

`\implies 3^(\log_3(x+5))=3^2`

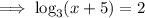
Apply the log law
`a^(\log_ax)=x` :

`\implies x+5=3^2`

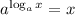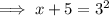
Swap sides:

`\implies 3^2=x+5`

Solve for x

Although the question hasn't asked to solve for x, here is the solution:

`\implies 3^2=x+5`

`\implies 9=x+5`

`\implies x=9-5`

`\implies x=4`

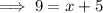
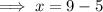
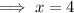
Check

Substitute the found value of x into the original equation:

`x=4 \implies \log_3(4+5)=\log_39=2 \quad \leftarrow\textsf{correct}`